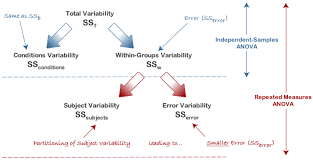
Calculating Sample Size Estimates – The Effect Size
There’s no question that some parts of running models are easier than others. And when talking about complexity or difficulty, we have to mention the effect size when you are calculating sample size estimates. One of the things that you may not know is that the power of every significance test is based on four … Read more