Confidence Intervals – z-scoretable.com

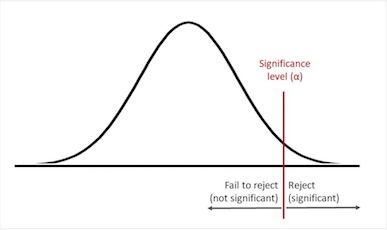
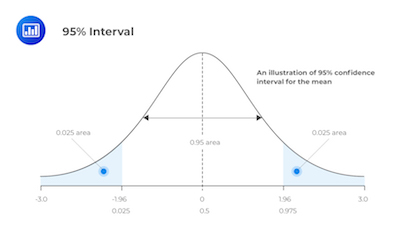
Significance Level Vs. Confidence Level Vs. Confidence Interval

October 29, 2020 by Eric Wong

While many assume statistics is a science, it really isn’t. After all, you probably already know that many terms are open to interpretation not to mention that many words mean the same thing such as man and average. But there are others that may appear to be the same and can be quite different such … Read more

What Is A Confidence Interval?

October 14, 2020 by Eric Wong

In statistics, a confidence interval refers to the probability of a population parameter fall between a set of values for a certain proportion of times. Generally speaking, a confidence interval measures the degree of certainty or uncertainty in a sampling method. Learn more about the Z-score. Notice that they can take any number of probability … Read more