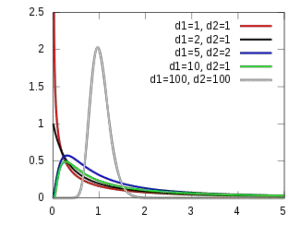
What is The F Distribution?
Overall speaking, a statistician needs to determine if a pattern he identified in the data is significantly different from no pattern at all. As you already know, there are many different ways to do this. However, the most common one involves using probability functions. Discover everything you need to know about the Z table. The … Read more