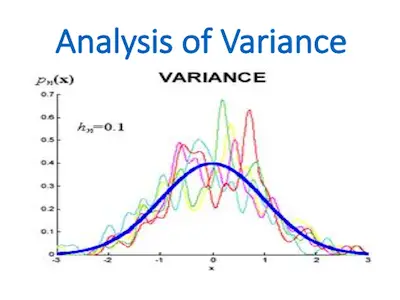
What is Variance?
When you’re studying statistics, it’s likely that you already heard about variance. After all, this is one of the first concepts you learn. Learn everything you need about z-score tables. What is Variance? Variance is simply a measurement of the spread between numbers in a data set. So, you can say that variance measures how … Read more