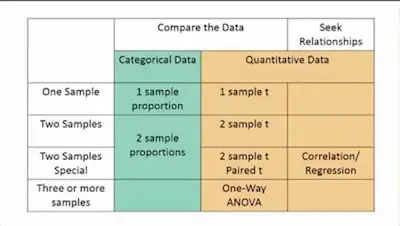
Statistical Tests – When To Use Which?
When you are studying statistics for the first time, you probably already realized that there is a wide range of statistical tests that you can perform. So, how can you know which statistical test you should conduct at any given time? Find your z score value here. Null Hypothesis And Testing Before we actually get … Read more