In statistics, there are many different types of probability distributions. While you tend to read and hear only about norma distribution, the reality is that there are others. Let’s take a closer look at them.
The Most Common Probability Distributions
#1: Normal Distribution:
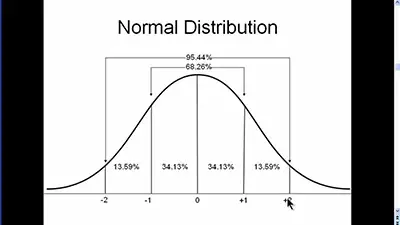
The normal distribution is the most common one. The truth is that the large sum of small random variables tend to be normally distributed. Here are some of the main characteristics of a normal distribution:
- The curve of the distribution features a bell shape and is symmetrical.
- The mean, mode, and median are equal.
- The total area under the curve is 1 or 100%.
- Half of the values will be to the left side of the center and the other half to the right.
Discover more details about the normal distribution.
#2: Bernoulli Distribution:
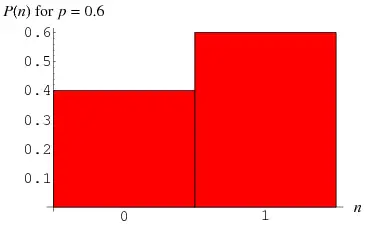
While the name may scare you, the truth is that this is one of the types of probability distributions that is easier to understand. Simply put, a Bernoulli distribution can only have two possible outcomes. They are 1 (success) and 0 (failure). And then you have a single trial.
So, the random variable x that has this type of distribution can take value 1 with the probability of success (p) and the value 0 with the probability of failure (q or 1-p).
Notice that the probabilities in this type of distribution don’t need to be equal. Some examples of Bernoulli distribution include knowing whether it is going to rain or not tomorrow.
Want to know more about the z score?
#3: Uniform Distribution:

The basis of an uniform distribution is that the probabilities of getting the different outcomes are equal. One simple example is when you roll a fair die.
One of the most interesting things about the uniform distribution is its graphical representation. Unlike the normal distribution that resembles a bell, the uniform distribution is rectangular. This is why this distribution is also known as a rectangular distribution.
Discover how to determine the z score value.
#4: Binomial Distribution:
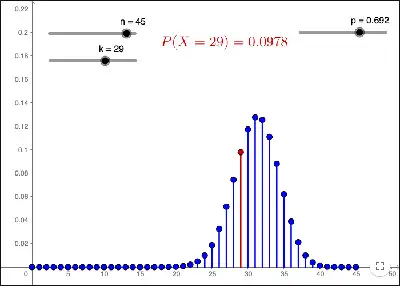
A binomial distribution occurs where there are only two possible outcomes such as win or lose, gain or loss, success or failure. Besides, the probability of success and failure are always the same for all trials. However, the results may be different. Some of the characteristics of the binomial distribution include:
- There are only two possible outcomes in a trial – success or failure.
- Each trail is independent.
- The probability of success and failure is the same for all trials.
- A total number of n identical trials are conducted.
#5: Poisson Distribution:
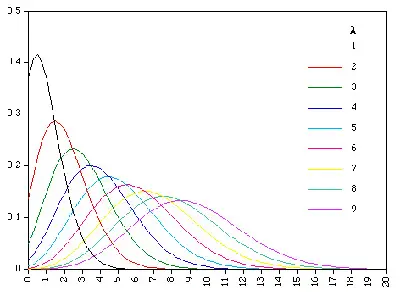
Discover more probability distribution types.
The Poisson distribution is applied to cases or situations where events can occur at random points of space and time wherein your interest lies only in the number of occurrences of the event. Some examples that can be modeled by the Poisson distribution include:
- The number of printing errors are each page of a book.
- The number of thefts in an area on a day.
- The number of calls that are made at a call center a day.
- The number of suicides reported in a specific city.
- The number of customers arriving at a restaurant in one hour.
- The number of emergency calls recorded at a hospital in a day.
